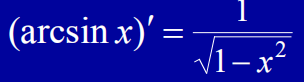【python与高等数学专题 一】Python3在一幅图绘制多个函数图像

（一）背景与应用

在高等数学等学科的学习与应用、数学分析与可视化等场景，我们时常会需要去将一个函数图像绘制出来以便于我们进行分析，通过Python3可以很方便地实现这一点，比起MATLAB等，其轻便、容易上手。

（二）用到的库

• matplotlib
• numpy

（三）通用代码

需求分析

我们需要一个能够在同一张图同时绘制多个函数图像的功能，以便于同时显示、对比和分析规律，因此我们先创建画布，随后根据采用plot函数进行绘制，根据函数的个数来实现多个函数的同时绘制在同一张画布上，设计的代码如下：

#!usr/bin/env python
# -*- conding:utf-8 -*-
import matplotlib.pyplot as plt
from numpy import linspace,sqrt,sin,cos,tan,arctan,pi,exp


def plotFunction(x,y,x2 = None,y2 = None,x3=None,y3 = None):
    fig = plt.figure(num = 1,dpi = 120)
    ax = plt.subplot(111)
    
    # 坐标轴
    ax = plt.gca()  # get current axis 获得坐标轴对象
    ax.spines['right'].set_color('none')  # 将右边 边沿线颜色设置为空 其实就相当于抹掉这条边
    ax.spines['top'].set_color('none')
    ax.xaxis.set_ticks_position('bottom')
    ax.yaxis.set_ticks_position('left')
    # 设置中心的为（0，0）的坐标轴
    ax.spines['bottom'].set_position(('data', 0))  # 指定 data 设置的bottom(也就是指定的x轴)绑定到y轴的0这个点上
    ax.spines['left'].set_position(('data', 0))

    
    ax.plot(x,y,label = "first Fig",color ="blueviolet")
    if x2 is not None and y2 is not None:
        ax.plot(x2,y2,label = "Second Fig",color ="red")
    #ax.set_xlim(0,2)
    ax.set_xlabel("line",color='cyan')
    #plt.draw()
    plt.legend()
    plt.show()

相关的参数、图像的调整可以参考Matplotlib手册，本文旨在于提供一个方法、思想。

（四）高等数学函数测试

以函数f(x)=sin(1/x)为例,首先定义一个函数以及函数定义域范围：

x = linspace(-2*pi,2*pi,1000)
y = sin(1/x)

plotFunction(x,y)

对于复杂的三角函数，如下图所示：

如果我们想知道这个函数的图像以及与上面的sin(1/x)的差异，我们只需要定义如下：

x = linspace(-2*pi,2*pi,1000)
y = sin(1/x)
y2 = sqrt(x)*(x**3-4*cos(x)-sin(1))

plotFunction(x,y,x,y2)

此函数还可以进行进一步的扩展，可以通过两个函数绘图实现原函数的绘制、一阶导函数等的绘制等功能。

x = linspace(-pi/2,pi/2,1000)
y = arcsin(x)
y2 = 1/sqrt(1-x*x)

plotFunction(x,y,x,y2)

其他功能可自行探索/改进。